How do we know that black holes are stable enough to sustain themselves? Click here to learn more about nature and proof of the existence of black holes! Astrophysics #1
Figure 1: Black hole
Introduction
In 1963, mathematician Roy Kerr laid the groundwork for the mathematical descriptions of space-time outside a rotating or spinning black hole. In the nearly six decades since his great achievement, scientists have been working extensively to show that these rotating black holes – called Kerr black holes – are stable. According to Jérémie Szeftel, a mathematician at Sorbonne University, “is that if I start with something that looks like a Kerr black hole and gives it a little bump” — by throwing some gravitational waves at it, for instance — “what you expect, far into the future, is that everything will settle down, and it will once again look exactly like a Kerr solution.”
If the opposition situation were to be experimentally verified – a mathematical instability – there would be a deep conundrum in fundamental physics and would have suggested “...the need to modify, at some fundamental level, Einstein’s theory of general relativity,” according to Thibault Damour, a physicist at the Institute of Advanced Scientific Studies in France.
The Breakthrough
Just recently, in a 912-page paper, Szeftel, Elena Giorgi of Columbia University, and Sergiu Klainerman of Princeton University mathematically proved that slowly rotating Kerr black holes are indeed stable. In addition to the new work, an 800-page paper by Klainerman and Szeftel from 2021 along with three other background papers established the necessary mathematical tools to confirm that black holes are stable – all the papers totalling roughly 2,100 pages.
In recent years, scientists have repeatedly confirmed predictions of general relativity through experimental observation. While Einstein proposed three classical tests to experimentally confirm relativity, scientists have seen observational confirmation of gravitational waves, binary pulsars, gravitational lensing, and black holes originally described by Karl Schwarzschild in 1916. This new result on stable black holes “does indeed constitute a milestone in the mathematical description of general relativity,” said Demetrios Christodoulou, a mathematician at the Swiss Federal Institute of Technology Zurich.
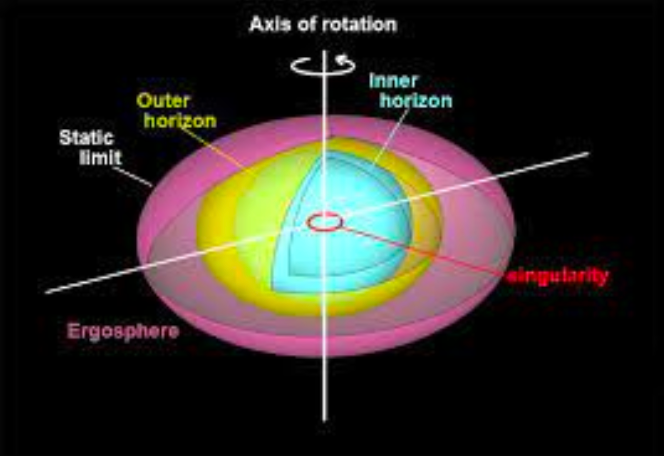
Why Now? How do Scientists Experimentally Verify Stable Black Holes?
One reason the question of stability has remained open for so long is that most explicit solutions to Einstein’s equations, such as the one found by Kerr, are stationary, according to Giorgi of Columbia University. Additionally, “These formulas apply to black holes that are just sitting there and never change; those aren’t the black holes we see in nature.” To assess stability, researchers need to subject black holes to minor disturbances and then see what happens to the solutions that describe these objects as time moves forward.
To better understand this, suppose we imagine sound waves hitting a wine glass. Almost always, the waves will shake the glass by varying amplitudes and frequencies, and then the system settles down. Now if someone sings loudly enough and at a pitch that exactly matches the glass’s resonant frequency – the natural frequency where a medium vibrates at the highest amplitude – the glass could shatter. In the case of stable black holes, a similar resonance-type phenomenon could happen when a black hole is struck by gravitational waves, according to Giorgi, Klainerman, and Szeftel.
Along with this, the three considered three possibilities to experimentally verify stable black holes through this approach. For instance, a gravitational wave might cross the event horizon of a Kerr black hole and enter the interior. The black hole’s mass and rotation could be slightly altered, but the object would still be a black hole characterized by Kerr’s equations. The gravitational waves, what’s more, could swirl around the black hole before dissipating in the same way that most sound waves dissipate after encountering a wineglass.
Figure 2: History of the universe with primordial black holes
The Importance of the Small Case to the Final State Conjecture
So far, stability has only been proven for slowly rotating black holes — where the ratio of the black hole’s angular momentum to its mass is much less than 1. It has not yet been demonstrated that rapidly rotating black holes are also stable. In addition, the researchers did not determine precisely how small the ratio of angular momentum to mass has to be in order to ensure stability.
Given that only one step in their long proof rests on the assumption of low angular momentum, Klainerman said he would “not be surprised at all if, by the end of the decade, we will have a full resolution of the Kerr [stability] conjecture.” Giorgi is not quite so sanguine. “It is true that the assumption applies to just one case, but it is a very important case.” Getting past that restriction will require quite a bit of work, she said; she is not sure who will take it on or when they might succeed.
Nevertheless, the stability of slowly rotating Kerr black holes plays a significant role in the final state conjecture, which basically suggests that if we wait long enough, the universe will evolve into a finite number of Kerr black holes moving away from each other. The final state conjecture, thus, depends on the stability of Kerr black holes and other small cases of conjectures – sub-conjectures. Understanding the final state conjecture will help us further understand physical cosmology and the end state of the universe according to the theories of Einstein, Kerr, and Schwarzschild. Black holes, moving forward, will command the attention of mathematicians and physicists for years, if not decades, to come.
Citations
Comments